1. Calcula el volumen de papel higiénico que hay en el siguiente rollo. Redondea a dos cifras decimales.
En primer lugar observemos que debemos calcular dos volúmenes. El volumen del cilindro formado por el papel y el volumen del cilindro hueco que aparece en el interior.
Una vez hecho esto deberemos restar el segundo al primero para calcular el volumen exacto de papel higiénico de que disponemos.
Cilindro completo
Como el diámetro mide 10 cm, el radio será de 5 cm.
Hueco
Como el diámetro mide 2 cm, el radio será de 1 cm.
Volumen de papel
V≅746.13 − 29.85 = 716.28 cm3
2. Volumen y área cilindro circunscrito en un prisma hexagonal de base un hexágono regular cuya apotema es de 2.6 cm y altura de 4 cm. Redondea a dos cifras decimales.
Para calcular el área y el volumen del cilindro necesitamos la altura (ya la tenemos) y el radio que obtenemos aplicando Pitágoras.
3. Calcular la altura de un cono de helado cuyo diámetro mide 5 cm y su volumen es de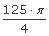 
m3. Redondea a dos cifras decimales.
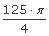m3. Redondea a dos cifras decimales.
Calculamos la altura del cono a partir del volumen:
El volumen de helado necesario será el volumen del cono calculado anteriormente más el volumen de la semiesfera que sobresale del cono
El área del papel será el área del cono pero con una altura de 15 − 3 = 12 cm. Calculamos la generatriz del cono por Pitágoras.
Para seguir aprendiendo:
No hay comentarios.:
Publicar un comentario
¿Cómo valoras mi blog? ¿Tienes algunas sugerencias?