El Teorema de Tales enuncia que si en un triángulo dado se traza un segmento paralelo a uno de sus tres lados, el nuevo triángulo generado será semejante al primero.
Al triángulo Δ ABC se le traza el segmento A’C’. Vemos que aparece un nuevo triángulo Δ A’BC’ semejante al primero. Tienen sus tres ángulos iguales y sus lados correspondientes son proporcionales.
De acuerdo con el teorema, se verifica que:
Esa razón de proporcionalidad se mantiene entre dos lados de un mismo triángulo y también entre los lados correspondientes del otro.

Ejemplo 1:
Nicolás mide 1,50 m. de altura, se encuentra a 1,20 m. de un poste que tiene encendida su luminaria a 3 m. del suelo, ¿cuál es el largo de la sombra que proyecta Nicolás?

Aplicamos el teorema de Thales;

El largo de la sombra que proyecta Nicolás es de 1,20 metros.
Ejemplo 2:

Ejemplo 3 :
Calcular la altura del edificio teniendo en cuenta los otros valores que son, la altura del árbol, la sombra que proyecta este y la distancia entre el edificio y donde termina la sombra del árbol.
El teorema de Tales sirve para resolver este tipo de ejercicios a los que se considera aplicaciones de Tales.
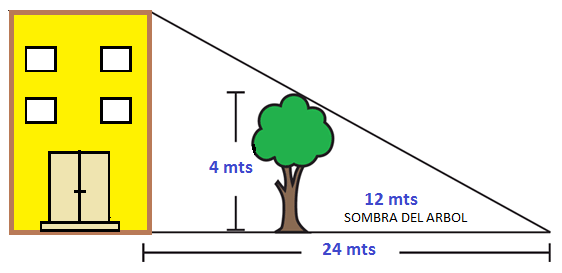
La relación que podemos establecer es la siguiente.
Llamamos x a la altura del edificio. Entonces la altura del edificio es a la altura del árbol como 24 es a 12.
X / 4 mts = 24 mts / 12 mts
X = (24 mts / 12 mts) . 4 mts
X = 8 mts
Ejemplo 4:
¿Cuál es la altura del montón de libros situado sobre el césped?

Si llamamos x a la altura de los libros aplicando el teorema de Tales,

Ya sabemos que el teorema de Tales puede utilizarse para medir grandes alturas o distancias inaccesibles, empleando la semejanza de triángulos.
por lo tanto las aplicaciones del teorema de Tales son muchas y muy importantes.
Para seguir aprendiendo:
Para seguir aprendiendo:










No hay comentarios.:
Publicar un comentario
¿Cómo valoras mi blog? ¿Tienes algunas sugerencias?