Teorema de Pitágoras.

Pitágoras

Pitágoras de Samos, fue un matemático y filósofo griego, nació en la isla de Samos, actual Grecia, en el año 572 a.C., fundó su escuela en Crotona en el sur de Italia. La escuela pitagórica era una sociedad o secta científica, religiosa y política. Los trabajos de los pitagóricos fueron desarrollados entre los años 585 a.C. y 400 a.C., existía un nivel de secreto en sus enseñanzas. Se dice que Pitágoras huyó a Metaponto, actual Italia, donde fue acecinado, en el año 497 a.C.

Teorema de Pitágoras.

En todo triángulo rectángulo, el cuadrado de la hipotenusa (lado opuesto al ángulo recto) es igual a la suma de los cuadrados de los catetos (lados que componen el ángulo recto).

Para entender mejor este teorema mira la siguiente representación donde se relacionan las áreas;

Recíproco del teorema de Pitágoras:

Del teorema principal de Pitágoras, se desprende el recíproco; Si en un triángulo, la suma de los cuadrados de dos de sus lados, es igual al cuadrado del tercer lado (el lado mayor), entonces es un triángulo rectángulo.

Dado el Δ ABC;

Entonces es un triangulo rectángulo es C.

Aplicaciones del teorema de pitágoras en la vida cotidiana.

Ejemplo 1:

Si un volantín ha quedado enredado en un poste de 6 metros de altura y el niño que lo tenía ha dejado el carrete en el suelo a 50 metros de este. ¿Cuánto hilo pierde si lo corta?

Primero puedes hacer un dibujo con lo que plantea el problema;

Para resolver este ejercicio podemos ocupar el teorema de Pitágoras de la siguiente forma;

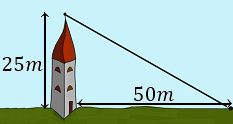
Ejemplo 2:

Se quiere colocar un cable desde la cima de una torre de 25 metros altura hasta un punto situado a 50 metros de la base la torre. ¿Cuánto debe medir el cable?

Solución:

c²= a²+b²
c²= 25²+ 50²
c²= 650+2500
c²= 3150
c= 56.12 metros.

Ejemplo 3:

Determinar cuántos metros tiene que caminar el Sr. González para llegar a su auto.

Solución:

c²= a²+b²
b²=c²-a²
b²=30²-24²
b²= 900-576
b²= 324
b= 18 metros.

Que bueno es saber que el teorema de pitágoras está inmerso en nuestro entono.

Acontinuación se te presenta un ejercicio para que puedas aplicar lo que estudiamos hoy, comenta cuál es tu respuesta.

Ejercicio:

Encontrar la distancia de donde está parado el señor González hasta la punta del árbol.

Para seguir aprendiendo:
Un programa de mucha utilidad.
http://www.aula365.com/